Pochodna funkcji jednej zmiennej - 24 sty
5.2 Punkty przegięcia funkcji
Teoria
Definicja
Punkt 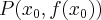 nazywamy punktem przegięcia funkcji
nazywamy punktem przegięcia funkcji  , jeżeli istnieje styczna do tej krzywej w punkcie
, jeżeli istnieje styczna do tej krzywej w punkcie 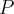 oraz funkcja ta jest
oraz funkcja ta jest
wypukła (wklęsła) na pewnym lewostronnym oraz wklęsła (wypukła) na pewnym prawostronnym sąsiedztwie punktu  .
.
Twierdzenie -- warunek konieczny istnienia punktu przegięcia
Jeżeli funkcja  ma ciągłą pochodną drugiego rzędu w punkcie
ma ciągłą pochodną drugiego rzędu w punkcie  oraz
oraz 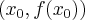
jest punktem przegięcia tej funkcji, to 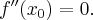
Twierdzenie -- I warunek wystarczający istnienia punktu przegięcia
Załóżmy, że funkcja  jest ciągła w punkcie
jest ciągła w punkcie  oraz dwukrotnie różniczkowalna na pewnym sąsiedztwie
oraz dwukrotnie różniczkowalna na pewnym sąsiedztwie  punktu
punktu  . Jeżeli wykres
. Jeżeli wykres  ma styczną w punkcie
ma styczną w punkcie 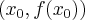 oraz
oraz
(1)  dla
dla  oraz
oraz  dla
dla 
lub
(2)  dla
dla  oraz
oraz  dla
dla  ,
,
to 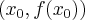 jest punktem przegięcia funkcji
jest punktem przegięcia funkcji  .
.
Twierdzenie -- II warunek wystarczający istnienia punktu przegięcia
Jeżeli funkcja  ma pochodną trzeciego rzędu w punkcie
ma pochodną trzeciego rzędu w punkcie  i spełnia jednocześnie warunki:
i spełnia jednocześnie warunki:
(1) 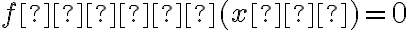 ,
,
(2) 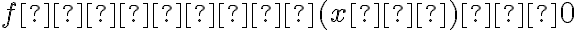 ,
,
(3) funkcja 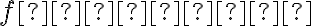 jest ciągła w punkcie
jest ciągła w punkcie  , to
, to 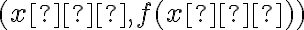 jest punktem przegięcia funkcji
jest punktem przegięcia funkcji  .
.