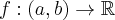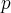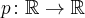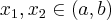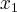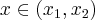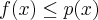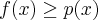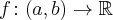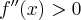Pochodna funkcji jednej zmiennej
5.1 Badanie wypukłości i wklęsłości funkcji
Teoria
Załóżmy, że funkcja  jest różniczkowalna na pewnym otoczeniu punktu
jest różniczkowalna na pewnym otoczeniu punktu  .
.
- wypukłą w punkcie
 , jeżeli istnieje takie sąsiedztwo
, jeżeli istnieje takie sąsiedztwo  punktu
punktu  , że dla każdego
, że dla każdego  zachodzi nierówność
zachodzi nierówność 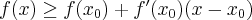 ;
; - wklęsłą w punkcie
 , jeżeli istnieje takie sąsiedztwo
, jeżeli istnieje takie sąsiedztwo  punktu
punktu  , że dla każdego
, że dla każdego  zachodzi nierówność
zachodzi nierówność 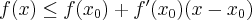 .
.
Jeżeli nierówności w powyższych definicjach są ostre, to funkcja jest odpowiednio ściśle wypukła lub ściśle wklęsła.
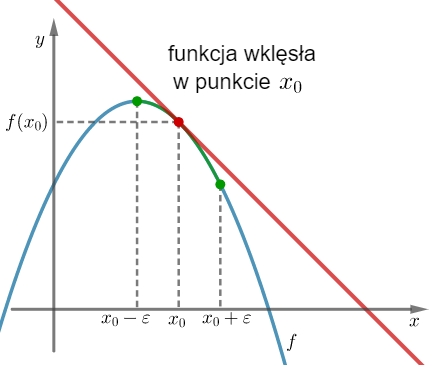
Geometrycznie oznacza to, że funkcja jest wypukła (wklęsła) w punkcie  , jeżeli istnieje takie sąsiedztwo
, jeżeli istnieje takie sąsiedztwo  , że na
, że na  wykres funkcji leży powyżej (poniżej) lub pokrywa się z prostą styczną do wykresu tej funkcji w punkcie
wykres funkcji leży powyżej (poniżej) lub pokrywa się z prostą styczną do wykresu tej funkcji w punkcie 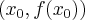 .
.
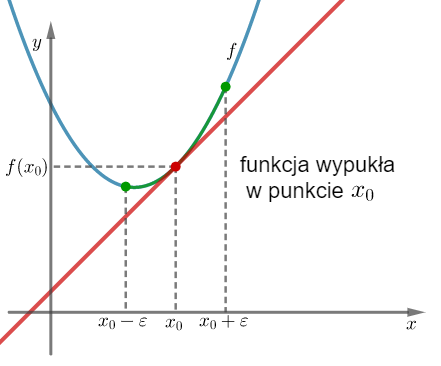
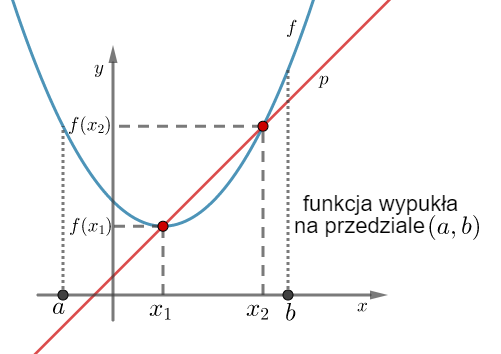
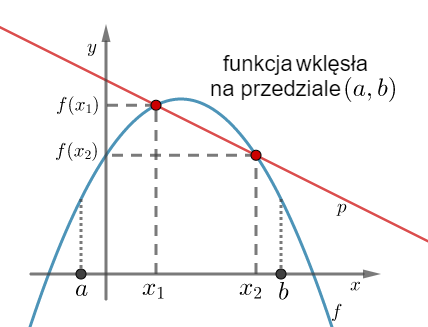
Geometrycznie oznacza to, że funkcja jest wypukła (wklęsła) na przedziale  , jeżeli na dowolnym przedziale
, jeżeli na dowolnym przedziale 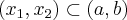 wykres funkcji leży pod (nad) lub pokrywa się z prostą sieczną przechodzącą przez punkty
wykres funkcji leży pod (nad) lub pokrywa się z prostą sieczną przechodzącą przez punkty 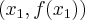 i
i 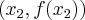 .
.