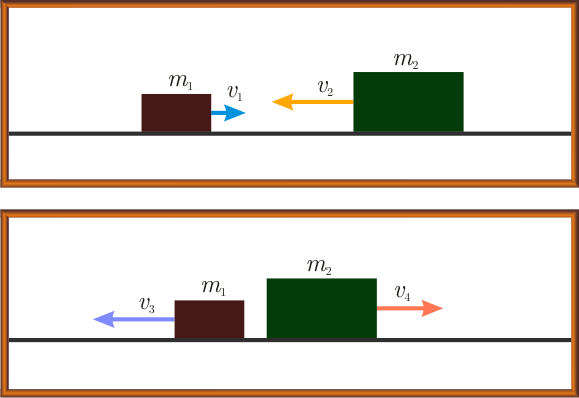
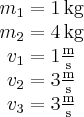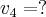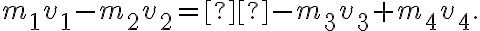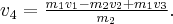Zachowanie pędu – zderzenie centralne; przykład
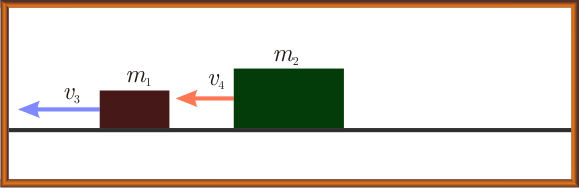
Dwa klocki poruszają się ku sobie i zderzają się centralnie. Znane są obie masy i wszystkie prędkości, oprócz prędkości drugiego klocka po zderzeniu.
Dane: Szukane:
Z zasady zachowanie pędu wynika
Z tego równania można wyznaczyć prędkość 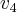
Podstawiając do tego wzoru dane otrzymamy 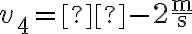 . Oznacza to, że w rzeczywistości drugi klocek porusza się w lewo z prędkością
. Oznacza to, że w rzeczywistości drugi klocek porusza się w lewo z prędkością