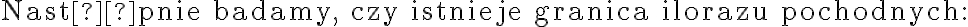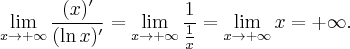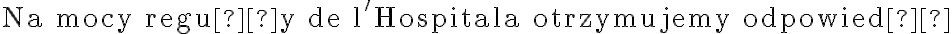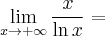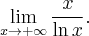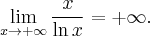Pochodna funkcji jednej zmiennej - styl1
| Strona: | WIKAMP Port |
| Przedmiot: | Pochodna funkcji jednej zmiennej |
| Książka: | Pochodna funkcji jednej zmiennej - styl1 |
| Wydrukowane przez użytkownika: | Gość |
| Data: | sobota, 7 marca 2026, 07:09 |
1. Wprowadzenie
Film:
Opis:
Kurza twarz
Przykład 1
Rozwiązanie
Przykład 1/w2
Rozwiązanie
Zaczynamy od określenia symbolu granicy, aby zdecydować, czy można zastosować regułę de l'Hospitala.
Następnie badamy, czy istnieje granica ilorazu pochodnych:
Na mocy reguły de l'Hospitala otrzymujemy odpowiedź:
To teraz po dodaniu stylu
Zaczynamy od określenia symbolu granicy, aby zdecydować, czy można zastosować regułę de l'Hospitala.
Następnie badamy, czy istnieje granica ilorazu pochodnych:
Na mocy reguły de l'Hospitala otrzymujemy odpowiedź:
1.1. Pochodna funkcji w punkcie
...
1.1.1. Teoria
...
1.1.2. Przykłady
...
1.1.3. Ćwiczenia interaktywne
...
1.2. Reguły różniczkowania
...
1.3. Interpretacja geometryczna pochodnej w punkcie
...
1.4. Interpretacja fizyczna i ekonomiczna pochodnej w punkcie
...
1.5. Zadania
...
2. Twierdzenia o wartości średniej i wnioski z nich
Film:
2.1. Twierdzenie Rolle'a i Lagrange'a
...
2.2. Reguła de l'Hospitala
...
2.3. Twierdzenie Taylora ?
...
2.4. Zadania
...
3. Monotoniczność funkcji, ekstrema lokalne i globalne
...
4. Rozdział drugi
Rozdział drugi.
Tekst drugiego rozdziału
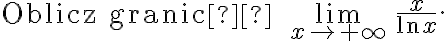
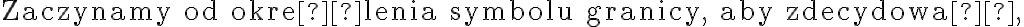
![\underset{x\rightarrow +\infty }{\lim }\, \dfrac{x}{\ln x} = \left[\dfrac{\infty}{\infty}\right]. \underset{x\rightarrow +\infty }{\lim }\, \dfrac{x}{\ln x} = \left[\dfrac{\infty}{\infty}\right].](https://port.edu.p.lodz.pl/filter/tex/pix.php/d7761b83a0950318f296f5a29c6ebe24.png)