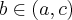Pochodna funkcji jednej zmiennej - 20.03
‒ o związku znaku pochodnej funkcji z monotonicznością funkcji
- Jeżeli
 dla każdego
dla każdego  , to funkcja
, to funkcja  jest stała na przedziale
jest stała na przedziale  .
. - Jeżeli
 dla każdego
dla każdego  , to funkcja
, to funkcja  jest rosnąca na przedziale
jest rosnąca na przedziale  .
. - Jeżeli
 dla każdego
dla każdego  , to funkcja
, to funkcja  jest malejąca na przedziale
jest malejąca na przedziale  .
. - Jeżeli
 dla każdego
dla każdego  , to funkcja
, to funkcja  jest niemalejąca na przedziale
jest niemalejąca na przedziale  .
. - Jeżeli
 dla każdego
dla każdego  , to funkcja
, to funkcja  jest nierosnąca na przedziale
jest nierosnąca na przedziale  .
.
1
Twierdzenie o związku znaku pochodnej funkcji z monotonicznością funkcji jest prawdziwe, gdy stosujemy je na przedziale. Natomiast w zbiorze będącym sumą rozłącznych przedziałów, to twierdzenie już nie zawsze jest prawdziwe.
Rozważmy np. funkcję  ,
,  . Pochodna tej funkcji jest równa
. Pochodna tej funkcji jest równa  dla
dla  . Zatem
. Zatem  dla każdego
dla każdego  . Funkcja jest więc malejąca na przedziale
. Funkcja jest więc malejąca na przedziale  i funkcja jest malejąca na przedziale
i funkcja jest malejąca na przedziale  . Natomiast nie jest prawdą, że funkcja
. Natomiast nie jest prawdą, że funkcja  jest malejąca na zbiorze
jest malejąca na zbiorze  .
.
![[a,b] [a,b]](https://port.edu.p.lodz.pl/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.png)