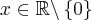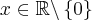Pochodna funkcji jednej zmiennej - 25 sty

    Przykład 1
    Pokażemy, że funkcja $f(x)=\frac{e^{x-2}}{x}$ nie posiada punktów przegięcia.
    Rozwiązanie:
    Dziedziną funkcji jest zbiór 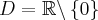$D=\mathbb{R}\backslash \left\{ 0\right\}$.
    Obliczamy pierwszą i drugą pochodną funkcji $f$:

$f^{\prime }(x)=\frac{e^{x-2}(x-1)}{x^{2}}$, $x\in \mathbb{R}\backslash \left\{ 0\right\}$,
$f^{\prime \prime }(x) =\frac{e^{x-2}(x^{2}-2x+2)}{x^{3}}$,  $x\in \mathbb{R}\backslash \left\{ 0\right\}\$

i przyrównujemy drugą pochodną do zera:

$f′′(x)=0 \iff \frac{e^{x-2}(x²-2x+2)}{x³}=0 \iff (e^{x-2}=0∨x²-2x+2=0)$. 
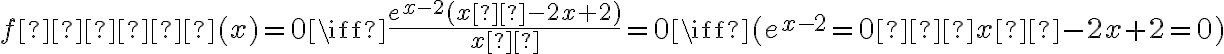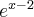
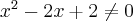Ponieważ $e^{x-2}$ $>0$ i $x^{2}-2x+2\neq0$ dla każdego $x\in\mathbb{R}\backslash \left\{ 0\right\}$, więc powyższe równanie nie posiada rozwiązania, zatem funkcja $f$ nie posiada punktów przegięcia.
    Przykład 2
    Pokażemy, że funkcja $f(x)=4x^3+8x\ln x$ nie posiada punktów przegięcia.
    Rozwiązanie:

    Dziedziną funkcji jest zbiór $D=(0, +\infty)$.
    Obliczamy pierwszą i drugą pochodną funkcji $f$:

$f'(x) =12x^2+8\ln x+8\text{ , }x\in (0, +\infty)$, 
$f''(x)=24x+\frac 8x$, $x\in (0, +\infty)$.
Zauważmy, że dla każdego 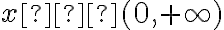$x∈(0, +\infty)$ pochodna rzędu drugiego jest dodatnia, zatem nie jest spełniony warunek konieczny istnienia punktu przegięcia i funkcja $f$ nie posiada punktów przegięcia.