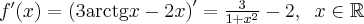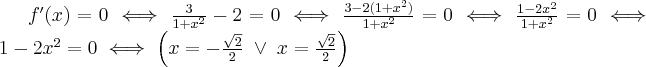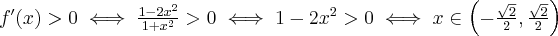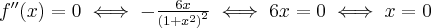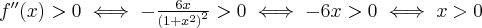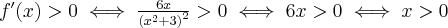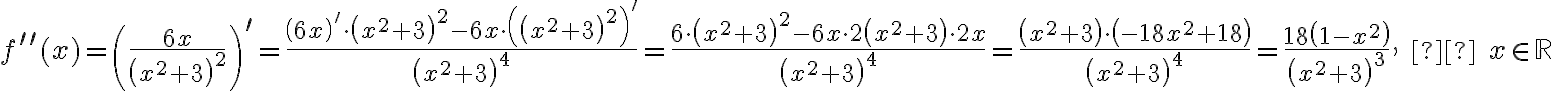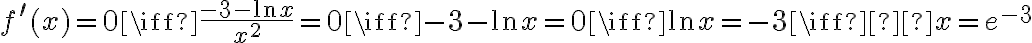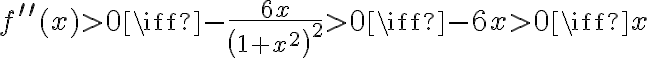Pochodna funkcji jednej zmiennej - 24 sty
6. Badanie przebiegu zmienności funkcji
Przykłady
-
Wyznaczymy asymptoty wykresu funkcji
 . Obliczamy w tym celu granice funkcji na krańcach jej dziedziny:
. Obliczamy w tym celu granice funkcji na krańcach jej dziedziny:Zatem prosta o równaniu
 jest asymptotą poziomą wykresu funkcji w
jest asymptotą poziomą wykresu funkcji w 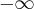 i
i 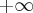 .
.Wykres funkcji nie ma asymptot pionowych.
-
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji
 . Obliczamy w tym celu pochodną funkcji.
. Obliczamy w tym celu pochodną funkcji.Wyznaczamy punkty stacjonarne funkcji:
Badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Zauważmy najpierw, że
 dla każdego
dla każdego  , zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia  . Mamy więc:
. Mamy więc:Zatem funkcja jest malejąca na przedziale
 , rosnąca na przedziale
, rosnąca na przedziale  .
.Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie
 funkcja ma minimum lokalne równe
funkcja ma minimum lokalne równe  .
. -
Wyznaczymy przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji
 . Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie
. Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie  .
.Badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie , a gdzie ujemne. Zauważmy, że
 dla każdego
dla każdego  , zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia  .
.Zatem funkcja jest wypukła na przedziale
 , wklęsła na przedziałach
, wklęsła na przedziałach  ,
,  . Punkty
. Punkty  ,
, 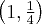 są punktami przegięcia funkcji.
są punktami przegięcia funkcji. -
Tabelka przebiegu zmienności funkcji
 .
.tabelka
-
wykres
- Dziedziną funkcji
 jest zbiór
jest zbiór  .
. - Wyznaczymy asymptoty wykresu funkcji
 . Obliczymy w tym celu granice funkcji na krańcach jej dziedziny:
. Obliczymy w tym celu granice funkcji na krańcach jej dziedziny: -
Zatem funkcja ma asymptotę pionową prawostronną
 ,
,Zatem prosta o równaniu
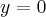 jest asymptotą poziomą wykresu funkcji
jest asymptotą poziomą wykresu funkcji  w
w 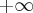 .
. -
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji
 . Obliczamy w tym celu pochodną funkcji.
. Obliczamy w tym celu pochodną funkcji.Wyznaczamy punkty stacjonarne funkcji:
Badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Zauważmy najpierw, że
 dla każdego
dla każdego  , zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia  . Mamy więc:
. Mamy więc:Zatem funkcja jest rosnąca na przedziale
 , malejąca na przedziale
, malejąca na przedziale  .
.Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie
 funkcja ma maksimum lokalne równe
funkcja ma maksimum lokalne równe  .
. -
Wyznaczymy przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji
 . Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie
. Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie  .
.Badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie , a gdzie ujemne. Zauważmy, że
 dla każdego
dla każdego  , zatem znak drugiej pochodnej funkcji będzie taki sam jak znak wyrażenia
, zatem znak drugiej pochodnej funkcji będzie taki sam jak znak wyrażenia  .
.Zatem funkcja
 jest wklęsła na przedziale
jest wklęsła na przedziale  , wypukła na przedziale
, wypukła na przedziale 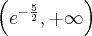 , punkt
, punkt 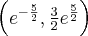 jest punktem przegięcia funkcji.
jest punktem przegięcia funkcji. -
Tabelka przebiegu zmienności funkcji f.
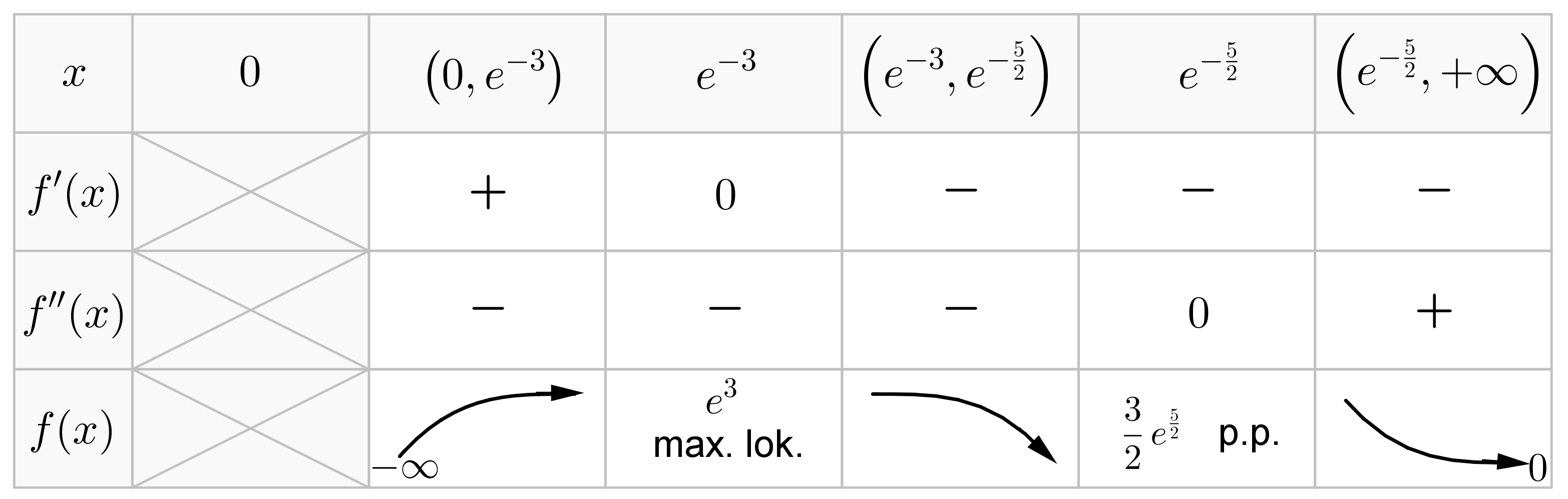
-
Wykres funkcji f.
wykres
- Dziedziną funkcji
 jest zbiór
jest zbiór  .
. -
Wyznaczymy asymptoty wykresu funkcji
 . Obliczymy w tym celu granice funkcji na krańcach jej dziedziny:
. Obliczymy w tym celu granice funkcji na krańcach jej dziedziny:Ponieważ obie policzone powyżej granice są niewłaściwe więc wykres funkcji nie ma symptpty poziomej. Sprawdzamy istnienie asymptot ukośnych wykresu funkcji w
 i
i  .
.Prosta o równaniu
 , czyli
, czyli  jest asymptotą ukośną wykresu funkcji w
jest asymptotą ukośną wykresu funkcji w 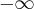 .
.Zatem prosta o równaniu
 jest asymptotą ukośną wykresu funkcji w
jest asymptotą ukośną wykresu funkcji w 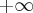 .
.Podsumowując otrzymujemy, że prosta o równaniu
 jest asymptotą ukośną wykresu funkcji w
jest asymptotą ukośną wykresu funkcji w 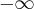 , prosta prosta o równaniu
, prosta prosta o równaniu  jest asymptotą ukośną wykresu funkcji w
jest asymptotą ukośną wykresu funkcji w 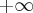 . Wykres funkcji
. Wykres funkcji  nie ma asymptot pionowych.
nie ma asymptot pionowych. -
Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji
 . Obliczamy w tym celu pochodną funkcji.
. Obliczamy w tym celu pochodną funkcji.Wyznaczamy punkty stacjonarne funkcji:
Badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Zauważmy najpierw, że
 dla każdego
dla każdego  , zatem znak pochodnej funkcji będzie taki sam jak znak wyrażenia
, zatem znak pochodnej funkcji będzie taki sam jak znak wyrażenia  . Mamy więc:
. Mamy więc:Zatem funkcja jest malejąca na każdym z przedziałów
 ,
, 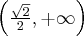 , rosnąca na przedziale
, rosnąca na przedziale  . Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie
. Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie 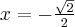 funkcja ma minimum lokalne, równe
funkcja ma minimum lokalne, równe 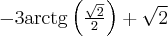 , w punkcie
, w punkcie  funkcja ma maksimum lokalne równe
funkcja ma maksimum lokalne równe 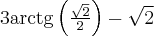 .
. -
Wyznaczymy przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji
 . Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie
. Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie  .
.Badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie , a gdzie ujemne. Zauważmy, że
 dla każdego
dla każdego  , zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia  .
.Zatem funkcja
 jest wypukła na przedziale
jest wypukła na przedziale  , wklęsła na przedziale
, wklęsła na przedziale  , w punkcie
, w punkcie  funkcja ma punkt przegięcia.
funkcja ma punkt przegięcia. -
Tabelka przebiegu zmienności funkcji f.
-
Wykres funkcji f.
wykres
Przykład 1
Zbadamy przebieg zmienności funkcji  .
.
Rozwiązanie
1. Dziedziną funkcji  jest zbiór
jest zbiór 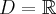 .
.
2. Wyznaczymy asymptoty wykresu funkcji  . Obliczamy w tym celu granice funkcji na krańcach jej dziedziny:
. Obliczamy w tym celu granice funkcji na krańcach jej dziedziny:
Zatem prosta o równaniu  jest asymptotą poziomą wykresu funkcji w
jest asymptotą poziomą wykresu funkcji w 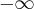 i
i 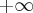 .
.
Wykres funkcji nie ma asymptot pionowych.
3. Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji  . Obliczamy w tym celu pochodną funkcji.
. Obliczamy w tym celu pochodną funkcji.
Wyznaczamy punkty stacjonarne funkcji:
Badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Zauważmy najpierw, że  dla każdego
dla każdego  , zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia  . Mamy więc:
. Mamy więc:
Zatem funkcja jest malejąca na przedziale  , rosnąca na przedziale
, rosnąca na przedziale  .
.
Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie  funkcja ma minimum lokalne równe
funkcja ma minimum lokalne równe  .
.
4. Wyznaczymy przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji  . Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie
. Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie  .
.
Badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie , a gdzie ujemne. Zauważmy, że  dla każdego
dla każdego  , zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia  .
.
Zatem funkcja jest wypukła na przedziale  , wklęsła na przedziałach
, wklęsła na przedziałach  ,
,  . Punkty
. Punkty  ,
, 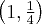 są punktami przegięcia funkcji.
są punktami przegięcia funkcji.
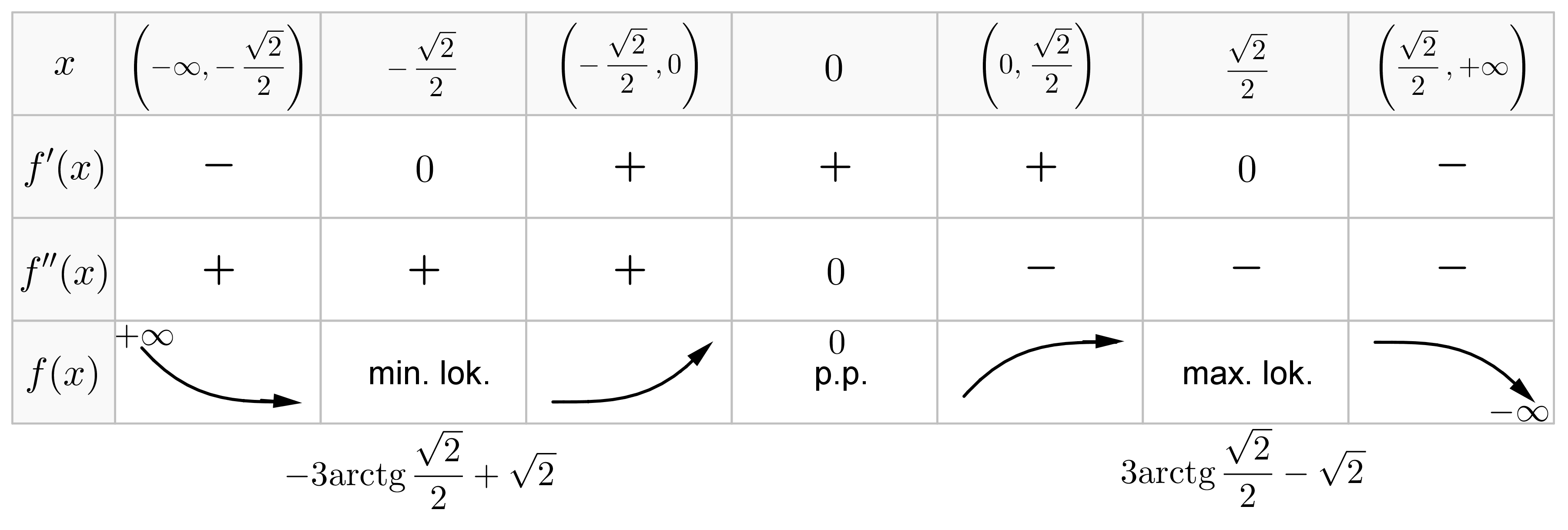
5. Tabelka przebiegu zmienności funkcji  .
.
Przykład 2
Zbadamy przebieg zmienności funkcji  .
.
1. Dziedziną funkcji  jest zbiór
jest zbiór  .
.
2.Wyznaczymy asymptoty wykresu funkcji  . Obliczymy w tym celu granice funkcji na krańcach jej dziedziny:
. Obliczymy w tym celu granice funkcji na krańcach jej dziedziny:
Zatem funkcja ma asymptotę pionową prawostronną  ,
,
Zatem prosta o równaniu 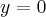 jest asymptotą poziomą wykresu funkcji
jest asymptotą poziomą wykresu funkcji  w
w 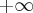 .
.
3. Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji  . Obliczamy w tym celu pochodną funkcji.
. Obliczamy w tym celu pochodną funkcji.
Wyznaczamy punkty stacjonarne funkcji:
Badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Zauważmy najpierw, że  dla każdego
dla każdego  , zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji pochodnej będzie taki sam jak znak wyrażenia  . Mamy więc:
. Mamy więc:
Zatem funkcja jest rosnąca na przedziale  , malejąca na przedziale
, malejąca na przedziale  .
.
Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie  funkcja ma maksimum lokalne równe
funkcja ma maksimum lokalne równe  .
.
4. Wyznaczymy przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji  . Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie
. Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie  .
.
Badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie , a gdzie ujemne. Zauważmy, że  dla każdego
dla każdego  , zatem znak drugiej pochodnej funkcji będzie taki sam jak znak wyrażenia
, zatem znak drugiej pochodnej funkcji będzie taki sam jak znak wyrażenia  .
.
Zatem funkcja  jest wklęsła na przedziale
jest wklęsła na przedziale  , wypukła na przedziale
, wypukła na przedziale 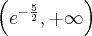 , punkt
, punkt 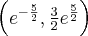 jest punktem przegięcia funkcji.
jest punktem przegięcia funkcji.
5. Tabelka przebiegu zmienności funkcji
6. Wykres funkcji
Przykład 3
Zbadamy przebieg zmienności funkcji 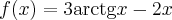 .
.
1. Dziedziną funkcji  jest zbiór
jest zbiór  .
.
2. Wyznaczymy asymptoty wykresu funkcji  . Obliczymy w tym celu granice funkcji na krańcach jej dziedziny:
. Obliczymy w tym celu granice funkcji na krańcach jej dziedziny:
Ponieważ obie policzone powyżej granice są niewłaściwe więc wykres funkcji nie ma symptpty poziomej. Sprawdzamy istnienie asymptot ukośnych wykresu funkcji w 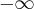 i
i 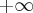 .
.
Prosta o równaniu  , czyli
, czyli  jest asymptotą ukośną wykresu funkcji w
jest asymptotą ukośną wykresu funkcji w 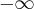 .
.
Zatem prosta o równaniu  jest asymptotą ukośną wykresu funkcji w
jest asymptotą ukośną wykresu funkcji w 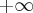 .
.
Podsumowując otrzymujemy, że prosta o równaniu  jest asymptotą ukośną wykresu funkcji w
jest asymptotą ukośną wykresu funkcji w 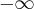 , prosta prosta o równaniu
, prosta prosta o równaniu  jest asymptotą ukośną wykresu funkcji w
jest asymptotą ukośną wykresu funkcji w 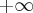 . Wykres funkcji
. Wykres funkcji  nie ma asymptot pionowych.
nie ma asymptot pionowych.
3. Wyznaczymy przedziały monotoniczności i ekstrema lokalne funkcji  . Obliczamy w tym celu pochodną funkcji.
. Obliczamy w tym celu pochodną funkcji.
Wyznaczamy punkty stacjonarne funkcji:
Badamy, gdzie pochodna funkcji przyjmuje wartości dodatnie, a gdzie ujemne. Zauważmy najpierw, że  dla każdego
dla każdego  , zatem znak pochodnej funkcji będzie taki sam jak znak wyrażenia
, zatem znak pochodnej funkcji będzie taki sam jak znak wyrażenia  . Mamy więc:
. Mamy więc:
Zatem funkcja jest malejąca na każdym z przedziałów  ,
, 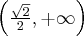 , rosnąca na przedziale
, rosnąca na przedziale  . Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie
. Korzystając z I warunku wystarczającego istnienia ekstremum funkcji wnioskujemy, że w punkcie 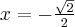 funkcja ma minimum lokalne, równe
funkcja ma minimum lokalne, równe 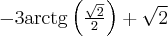 , w punkcie
, w punkcie  funkcja ma maksimum lokalne równe
funkcja ma maksimum lokalne równe 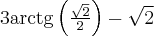 .
.
4. Wyznaczymy przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji  . Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie
. Obliczamy w tym celu drugą pochodną funkcji, następnie rozwiązujemy równanie  .
.
Badamy, gdzie druga pochodna funkcji przyjmuje wartości dodatnie , a gdzie ujemne. Zauważmy, że  dla każdego
dla każdego  , zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia
, zatem znak funkcji drugiej pochodnej będzie taki sam jak znak wyrażenia  .
.
Zatem funkcja  jest wypukła na przedziale
jest wypukła na przedziale  , wklęsła na przedziale
, wklęsła na przedziale  , w punkcie
, w punkcie  funkcja ma punkt przegięcia.
funkcja ma punkt przegięcia.
5. Tabelka przebiegu zmienności funkcji
6. Wykres funkcji

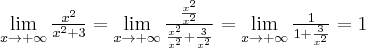

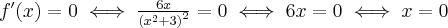
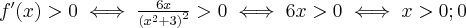

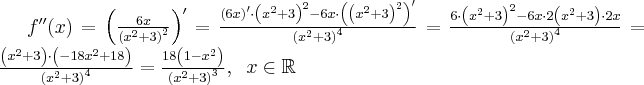
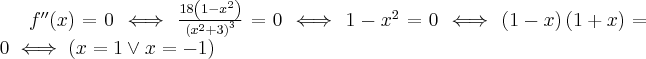


![\lim\limits_{x\to 0^+} \frac{4+\ln x}{x}=\left[\frac{4+\ln 0^+}{0^+}=\frac{4-\infty}{0^+}=-\infty\cdot (+\infty)\right]=-\infty \lim\limits_{x\to 0^+} \frac{4+\ln x}{x}=\left[\frac{4+\ln 0^+}{0^+}=\frac{4-\infty}{0^+}=-\infty\cdot (+\infty)\right]=-\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/fa58739fccd8b19164ec389009a2c7ab.png)
![\lim\limits_{x\to+ \infty} \frac{4+\ln x}{x}=\left[\frac{+\infty}{+\infty}\right]\stackrel{[H]}{=}\lim\limits_{x\to +\infty}\frac{\frac1x}{1}=\lim\limits_{x\to +\infty}\frac{1}{x}=\left[\frac{1}{+\infty}\right]=0 \lim\limits_{x\to+ \infty} \frac{4+\ln x}{x}=\left[\frac{+\infty}{+\infty}\right]\stackrel{[H]}{=}\lim\limits_{x\to +\infty}\frac{\frac1x}{1}=\lim\limits_{x\to +\infty}\frac{1}{x}=\left[\frac{1}{+\infty}\right]=0](https://port.edu.p.lodz.pl/filter/tex/pix.php/d9448ffb6c1a09ff78f17d7908456b2a.png)
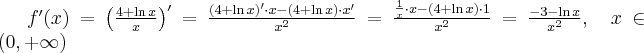
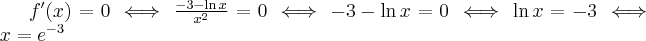
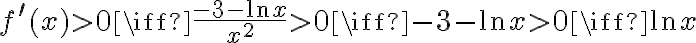
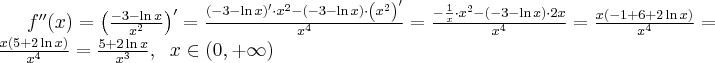
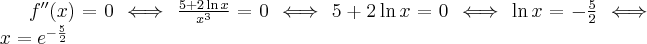
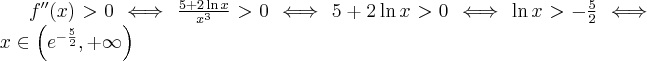
![\lim\limits_{x\to -\infty} f(x)=\lim\limits_{x\to -\infty}\left(3\mathrm{arctg}x-2x\right)=\left[{3\mathrm{arctg}(-\infty)-2\cdot(-\infty)=\frac {-3\pi}{2}}+\infty\right]=+\infty \lim\limits_{x\to -\infty} f(x)=\lim\limits_{x\to -\infty}\left(3\mathrm{arctg}x-2x\right)=\left[{3\mathrm{arctg}(-\infty)-2\cdot(-\infty)=\frac {-3\pi}{2}}+\infty\right]=+\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/93af07a6a6533f14b682ad6a550c74d9.png)
![\lim\limits_{x\to+ \infty} f(x)=\lim\limits_{x\to+ \infty}\left(3\mathrm{arctg}x-2x\right)=\left[{3\mathrm{arctg}(+\infty)-2\cdot\infty=\frac {3\pi}{2}}-\infty\right]=-\infty \lim\limits_{x\to+ \infty} f(x)=\lim\limits_{x\to+ \infty}\left(3\mathrm{arctg}x-2x\right)=\left[{3\mathrm{arctg}(+\infty)-2\cdot\infty=\frac {3\pi}{2}}-\infty\right]=-\infty](https://port.edu.p.lodz.pl/filter/tex/pix.php/b2edf6551dd37856e565d61e0a2e82db.png)
![\lim\limits_{x\to -\infty}\frac{f(x)}{x}= \lim\limits_{x\to -\infty}\frac{3\mathrm{arctg}x-2x}{x}=\lim\limits_{x\to -\infty} \frac{3\mathrm{arctg}x}{x}-2=\left[\frac{3\mathrm{arctg}(-\infty)}{-\infty}-2=\frac{-\frac {3\pi}{2}}{-\infty}-2\right]=-2 \Rightarrow a=-2 \lim\limits_{x\to -\infty}\frac{f(x)}{x}= \lim\limits_{x\to -\infty}\frac{3\mathrm{arctg}x-2x}{x}=\lim\limits_{x\to -\infty} \frac{3\mathrm{arctg}x}{x}-2=\left[\frac{3\mathrm{arctg}(-\infty)}{-\infty}-2=\frac{-\frac {3\pi}{2}}{-\infty}-2\right]=-2 \Rightarrow a=-2](https://port.edu.p.lodz.pl/filter/tex/pix.php/c74768032ee72d603f38fca86defafbe.png)
![\lim\limits_{x\to -\infty}(f(x)-ax)=\lim\limits_{x\to -\infty} \left(3\mathrm{arctg}x-2x-(-2x)\right)=\lim\limits_{x\to -\infty} 3\mathrm{arctg}x=\left[3\mathrm{arctg}(-\infty)\right]=\frac {-3\pi}{2}\Rightarrow b=\frac {-3\pi}{2} \lim\limits_{x\to -\infty}(f(x)-ax)=\lim\limits_{x\to -\infty} \left(3\mathrm{arctg}x-2x-(-2x)\right)=\lim\limits_{x\to -\infty} 3\mathrm{arctg}x=\left[3\mathrm{arctg}(-\infty)\right]=\frac {-3\pi}{2}\Rightarrow b=\frac {-3\pi}{2}](https://port.edu.p.lodz.pl/filter/tex/pix.php/e021c47815267205199c2f6f510dd128.png)
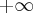
![\lim\limits_{x\to +\infty}\frac{f(x)}{x}= \lim\limits_{x\to +\infty}\frac{3\mathrm{arctg}x-2x}{x}=\lim\limits_{x\to +\infty} \frac{3\mathrm{arctg}x}{x}-2=\left[\frac{3\mathrm{arctg}(+\infty)}{+\infty}-2=\frac{\frac {3\pi}{2}}{+\infty}-2\right]=-2 \Rightarrow a=-2 \lim\limits_{x\to +\infty}\frac{f(x)}{x}= \lim\limits_{x\to +\infty}\frac{3\mathrm{arctg}x-2x}{x}=\lim\limits_{x\to +\infty} \frac{3\mathrm{arctg}x}{x}-2=\left[\frac{3\mathrm{arctg}(+\infty)}{+\infty}-2=\frac{\frac {3\pi}{2}}{+\infty}-2\right]=-2 \Rightarrow a=-2](https://port.edu.p.lodz.pl/filter/tex/pix.php/54970a2305335fa5edd6239d9b459125.png)
![\lim\limits_{x\to+ \infty}(f(x)-ax)=\lim\limits_{x\to +\infty} \left(3\mathrm{arctg}x-2x-(-2x)\right)=\lim\limits_{x\to +\infty} 3\mathrm{arctg}x=\left[3\mathrm{arctg}(+\infty)\right]=\frac {3\pi}{2}\Rightarrow b=\frac {3\pi}{2} \lim\limits_{x\to+ \infty}(f(x)-ax)=\lim\limits_{x\to +\infty} \left(3\mathrm{arctg}x-2x-(-2x)\right)=\lim\limits_{x\to +\infty} 3\mathrm{arctg}x=\left[3\mathrm{arctg}(+\infty)\right]=\frac {3\pi}{2}\Rightarrow b=\frac {3\pi}{2}](https://port.edu.p.lodz.pl/filter/tex/pix.php/cefdac3e7b1415bf6e71ef4e43964e3a.png)