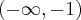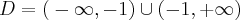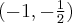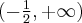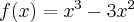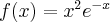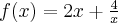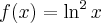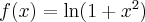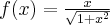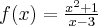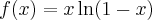Pochodna funkcji jednej zmiennej
5. Wypukłość, wklęsłość funkcji, punkty przegięcia
5.3 Zadania
1
2
3
 Punkt przegięcia:
Punkt przegięcia: 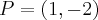 . Funkcja jest wypukła na przedziale
. Funkcja jest wypukła na przedziale 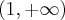 , wklęsła na przedziale
, wklęsła na przedziale 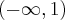 .
.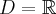 . Punkty przegięcia:
. Punkty przegięcia: 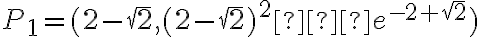 ,
, 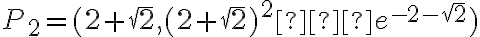 . Funkcja jest wypukła na przedziałach
. Funkcja jest wypukła na przedziałach 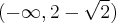 ,
, 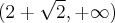 , wklęsła na przedziale
, wklęsła na przedziale 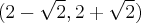 .
.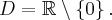 Brak punktów przegięcia. Funkcja jest wypukła na przedziale
Brak punktów przegięcia. Funkcja jest wypukła na przedziale  , wklęsła na przedziale
, wklęsła na przedziale  .
. . Punkt przegięcia:
. Punkt przegięcia: 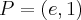 . Funkcja jest wypukła na przedziale
. Funkcja jest wypukła na przedziale 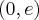 , wklęsła na przedziale
, wklęsła na przedziale 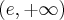 .
.
4
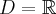 . Punkty przegięcia:
. Punkty przegięcia: 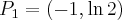 ,
, 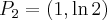 . Funkcja jest wypukła na przedziale
. Funkcja jest wypukła na przedziale 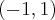 , wklęsła na przedziałach
, wklęsła na przedziałach 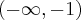 ,
, 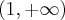 .
. Punkt przegięcia:
Punkt przegięcia: 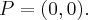 Funkcja jest wypukła na przedziale
Funkcja jest wypukła na przedziale 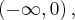 wklęsła na przedziale
wklęsła na przedziale 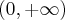 .
.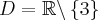 . Brak punktów przegięcia. Funkcja jest wypukła na przedziale
. Brak punktów przegięcia. Funkcja jest wypukła na przedziale 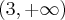 , wklęsła na przedziale
, wklęsła na przedziale 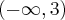 .
.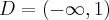 . Brak punktów przegięcia. Funkcja jest wklęsła na na przedziale
. Brak punktów przegięcia. Funkcja jest wklęsła na na przedziale 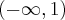 .
.

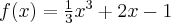
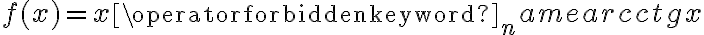
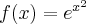
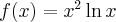


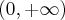
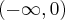
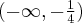
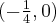
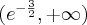
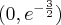
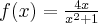
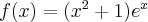
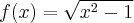
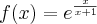
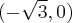
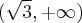
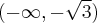
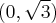
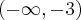
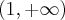

![D=\mathbb{(}-\infty ,-1]\cup \lbrack 1,+\infty ) D=\mathbb{(}-\infty ,-1]\cup \lbrack 1,+\infty )](https://port.edu.p.lodz.pl/filter/tex/pix.php/51b15beb33b9ffe9bea68cdebad4f543.png)