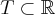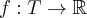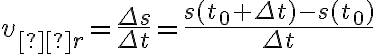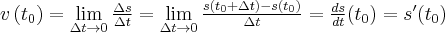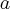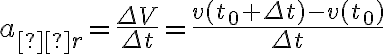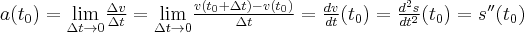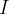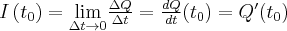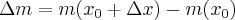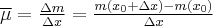Pochodna funkcji jednej zmiennej

Dokładniejszą charakterystykę szybkości zmian funkcji otrzymamy wtedy, gdy w powyższym ilorazie przejdziemy do granicy. Konieczna jest jednak znajomość analitycznego wzoru rozważanej funkcji.

Potrzebę wprowadzenia pochodnej objaśnimy na przykładzie fizycznych wielkości:

 

1. Prędkość $v$

Rozpatrzmy ruch po linii prostej, aby nie trzeba się było posługiwać wektorami.

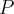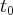Wyobraźmy sobie punkt materialny $P$ poruszający się ze zmienną prędkością po osi liczbowej $s$ w taki sposób, że jego pozycja w chwili $t_{0}$ określona jest jako funkcja czasu i wynosi 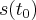$s(t_{0})$. W chwili 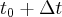$t_{0}+\Delta t$ współrzędna (pozycja) tego punktu jest równa 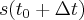$s(t_{0}+\Delta t)$. Przesunięcie w czasie 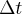$\Delta t$ jest równe 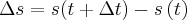$\Delta s=s(t+\Delta t)-s\left( t\right)$. Zatem prędkość średnia jest równa

$v_{śr} =\frac{\Delta s}{\Delta t}=\frac{s(t_{0}+\Delta t)-s(t_{0})}{\Delta t}$,

zaś prędkość chwilowa w chwili 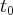$t_{0}$ jest równa

$v\left( t_{0}\right) =\lim\limits_{ \Delta t\to 0}\frac{\Delta s}{\Delta t}= \lim\limits_{\Delta t\to 0}\frac{s(t_{0}+\Delta t)-s(t_{0})}{\Delta t}=\frac{ds}{dt}(t_0)=s'(t_{0})$.

2. Przyspieszenie $a$

W czasie 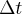$\Delta t$ punkt materialny 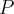$P$ przyspieszy od chwili 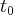$t_0$ do chwili 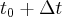$t_0+\Delta t$ średnio o

$a_{śr}=\frac{\Delta V}{\Delta t}=\frac{v(t_{0}+\Delta t)-v(t_{0})}{\Delta t}$.

Granicę właściwą tego ilorazu różnicowego, gdy 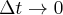$\Delta t\to 0$ nazywamy przyspieszeniem punktu 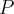$P$ w chwili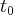 $t_0$

$a(t_{0})=\underset{\Delta t\to 0}{\lim }\frac{\Delta v}{\Delta t}=\underset{\Delta t\to 0}{\lim }\frac{v(t_{0}+\Delta t)-v(t_{0})}{\Delta t}=\frac{dv}{ dt}(t_{0})=\frac{d^2s}{dt^2}(t_0)=s''(t_{0})$.

3. Natężenie prądu $I$

Prąd elektryczny to uporządkowany ruch ładunków elektrycznych wzdłuż przewodnika. Niech 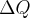$\Delta Q$ oznacza ładunek przepływający przez ustalony przekrój przewodnika w czasie 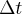$\Delta t$. Wówczas wielkość 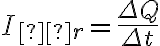$I_{śr}=\frac{\Delta Q}{\Delta t}$ nazywa się średnim natężeniem prądu. Chwilowym natężeniem prądu jest wielkość

$I\left( t_{0}\right) =\underset{\Delta t\to 0}{\lim }\frac{\Delta Q}{ \Delta t}=\frac{dQ}{dt}(t_{0})=Q'(t_{0})$.

4. Gęstość rozkładu masy $μ$

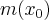Załóżmy, że mamy pręt o długości $L$ taki, że masa części tego pręta liczona od początku do punktu $x_0\in[0,L]$ dana jest funkcją $m(x_0)$. Wtedy masa zawarta w przedziale $[x_0,x_0+\Delta x]$ wynosi:

$\Delta m=m(x_{0}+\Delta x)-m(x_{0})$.

Średnia gęstość masy na tym przedziale jest równa:

$\overline{\mu }=\frac{\Delta m}{\Delta x}=\frac{m(x_{0}+\Delta x)-m(x_{0})}{\Delta x}$.

W granicy otrzymuje się gęstość masy w punkcie $x_0$

$\mu \left( x_{0}\right) =\underset{\Delta x\rightarrow 0}{\lim }\frac{\Delta m}{\Delta x}=m'(x_{0})$.